統計學概念疑問-假設檢定的誤差類型 等問題
你好,我統計學基礎比較弱, 目前到 假設檢定的誤差類型 等問題就卡住了, 1. H0、H1 為什麼可以劃出重疊的常態分配曲線圖? 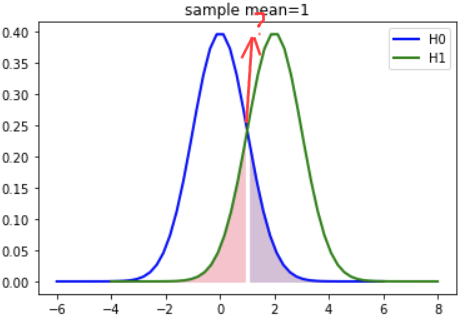 2. p – value 公式如何計算? 這是我參考的p – value 公式教學: https://chih-sheng-huang821.medium.com/%E7%B5%B1%E8%A8%88%E5%AD%B8-%E5%A4%A7%E5%AE%B6%E9%83%BD%E5%96%9C%E6%AD%A1%E5%95%8F%E7%9A%84%E7%B3%BB%E5%88%97-p%E5%80%BC%E6%98%AF%E4%BB%80%E9%BA%BC-2c03dbe8fddf 但我不明白 伽瑪函數(Gamma函數) 的計算 比如它範例1中 如何用伽瑪函數(Gamma函數)如何把這值計算成 0.398? 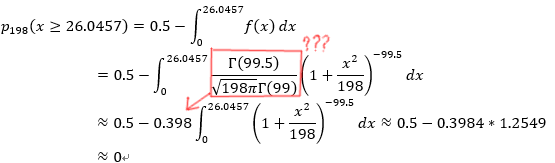 請問可以這可以在哪裡參考? 或是該怎麼理解?
回答列表
-
2021/04/07 下午 02:00Paul贊同數:3不贊同數:0留言數:0
1. H0和H1所假定的值都是隨機變數,所以有統計分佈,亦即圖中常態分佈的曲線。峰值即是平均值 。 2. p值其實就是型一誤差的機率,計算的方法和分布有關,常態分佈的話可用由Z-分數(Z-score)求p得出,或直接套用 https://www.statsmodels.org/stable/generated/statsmodels.stats.proportion.proportions_ztest.html 不大會需要自己算。
-
2021/04/07 下午 05:44Jaio贊同數:2不贊同數:0留言數:0
1. H0、H1 為什麼可以劃出重疊的常態分配曲線圖? 答 : 這只是示意圖,不一定是常態的! 他們是根據「檢定統計量」所決定的圖,實際操作中,把H0的u帶入檢定統計的分布即可把H0的圖畫出,而H1沒有固定的值所以實際上無法畫。另外,型一錯誤的機率就是紫色那塊,而型二錯誤是紅色那塊。 2. p – value 公式如何計算? 答: 我們用 python 計算吧,不過計算這個之前,要先了解 gamma function,我們用到了對於n為正整數的定義 nf(n) = f(n+1) 與 f(1/2) = \sqrt{2} ```python import math import numpy as np ``` ``` def ga(x): # gamma 函數 (xf(x) = f(x+1)) num = 1 if x == 1/2: num = num * math.sqrt(np.pi) else: while x>1 : x = x-1 if x == 1/2: num = num * x * math.sqrt(np.pi) break else: num = num*x return num ``` 以下函數適用範圍: {(x,y) | x,y > 0.5 a nd 0.5|x and 0.5|y} ``` def qp(x,y): # gamma(x)/gamma(y) (不直接用兩個 gamma 函數直接相除是因為怕數字太大而且能算得更精確) ans = 1 while True: try: if y == 0.5: ans = ans / math.sqrt(np.pi) * ga(x) break elif x == 0.5: ans = ans * math.sqrt(np.pi) * ga(y) break elif min(x,y) == 1: ans = ans * ga(max(x,y)) break else: x = x-1 y = y-1 ans = ans * x/y except: break return ans ``` ``` # 計算問題2 round(qp(99.5,99)/math.sqrt(198*np.pi)) # round( number we want to know,4) 可以取到小數點後四位 output : 0.3984 ``` 若想了解有關 gamma function 相關定理與性質,我覺得這篇寫得很好,可以參考看看 : https://brilliant.org/wiki/gamma-function/ 以上若有錯誤歡迎糾正~
