【QA】Backpropagation 背後的數學推導過程是什麼?
很多在學習深度學習的人,第一個會卡到的點往往是Backpropagation. 但請別把它想得太過複雜,就把它想成"效率比較高的Gradient Descent"就好的,不同於forward pass的從頭到尾,Backpropagation顧名思義, 是從最後一顆神經元的Gradient開始觀察,再搭配Chain Rule來做比較有效率的Optimization。
回答列表
-
2021/11/10 下午 01:49Kevin Luo贊同數:0不贊同數:0留言數:0
解說: 以下, 是一個大型神經網路: 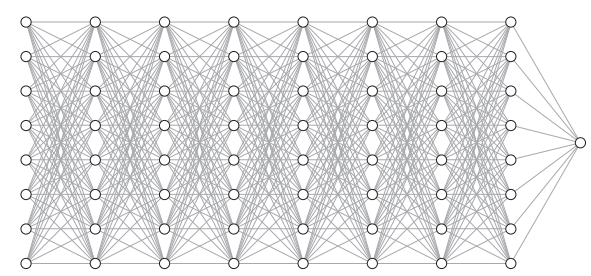 我們取上圖的一小部分3乘3的網路來舉例: 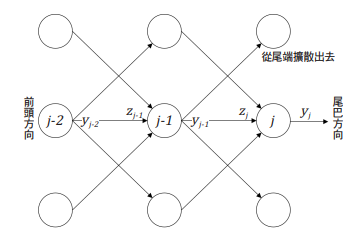 Backpropagation 的 Chain Rule 基本過程圖示化如下: 開始詳細說明: 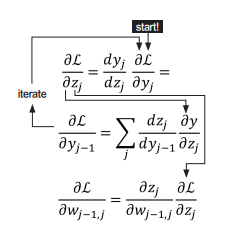 從神經網路的任一個neuron j開始,一開始∂Γ/yj 我們先計算損失函數Γ(gamma)對該neuron j 的輸出yj的變化率∂Γ/ ∂yj,運用chain rule我們就可以再算出Γ對neuron j 的輸入Zj的變化率: 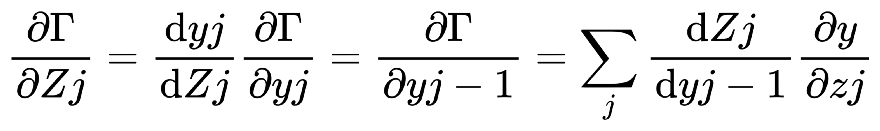 (請注意! 這裡的yj和yj-1中的j和j-1都是下標,表示第j顆神經元和第j-1顆! 並非相乘!) 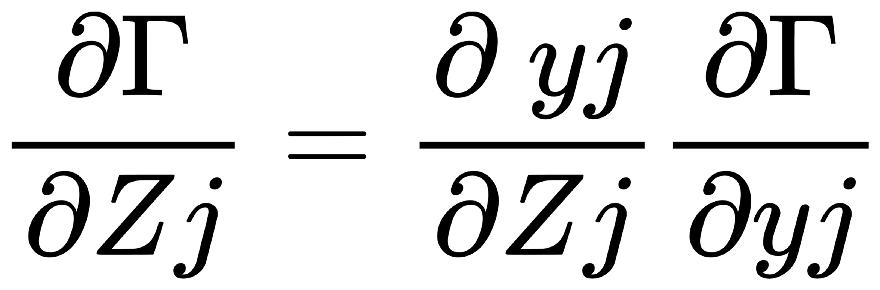 觀察上式: 其中∂Γ/ ∂yj 是已知,所以我們只要算 ∂yj/ ∂Zj就好了, 而yj是在forward pass就已經算好了。 所以 ∂yj/ ∂Zj很快就可以"秒算"出來了。 而 ∂Γ/ ∂Zj 就只是將∂yj/ ∂Zjc和∂Γ/ ∂yj相乘而已。 接著來算前一個(從順率算Zj的前一個就是yj-1): 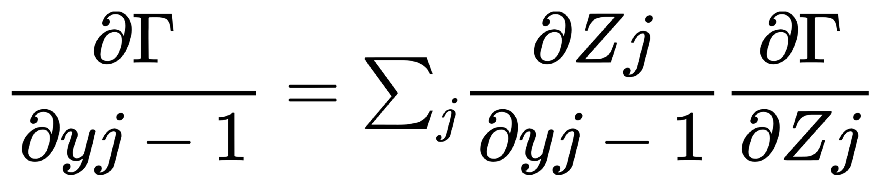 或許有人會confuse,為甚麼要有Summation Σ 呢? 因為Zj 對 loss function Γ 的影響會從 neuron j 所在的那一層的各個neuron往尾端的各neuron(各路線)擴散出去,所以要每條線都加起來。這其實就是"多變數Chain Rule"的概念。 然後…接下來就用Chain rule的方式如法炮製: 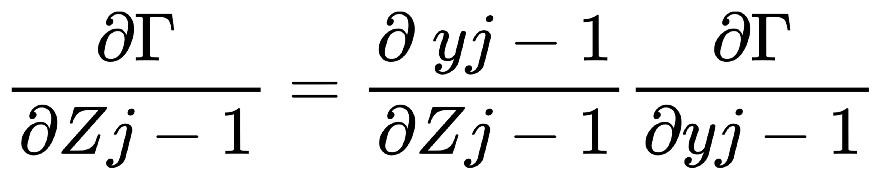 這裡一樣把算好的∂Γ/∂yj-1拿來乘就好, 而yj-1已經在forward pass算好了, 所以只要算∂yj-1/∂Zj-1就好了! 同樣的動作: 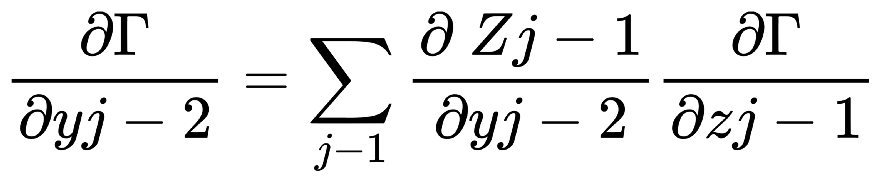 以此類推下去… 所以按照這樣從 j → j-1 → j-2… 就可以把全部neuron的輸入對 loss function Γ 的影響率(∂Γ/∂zj)和輸出對loss function Γ的影響率 (∂Γ/∂yj)都給算出來,這就是偏微分 chain rule 做反向傳播(Backpropagation)的過程。 但是不要忘了,我們最後的目的是要得到 loss function對權重的偏微分, 即∂Γ/∂Wj !! 因為我們最終要用Gradient Descent來優化Wj ==> Wj = Wj - η(∂Γ/∂Wj) 來改變一點點的Wj值, 以便用SGD !!! 算∂Γ/∂Wj可以說是前述反向傳播法的副產品, 因為: 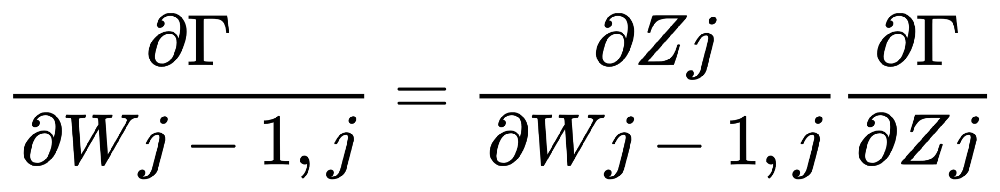 其中∂Γ/∂Zj我們已經算出來了,而Zj和Wj-1,j的關係是: Zj = (Wj-1,j )*( yj-1) + bj-1,j ==> ∂Zj/∂Wj-1,j = yj-1 (Wj-1,j 微分後變1,bj-1,j微分後變0) => ∂Γ/∂Wj-1,j = yj-1*∂Γ/∂Zj 其中∂Γ/∂Zj已經算好了, yj-1也在向前傳播時算好了, 所以∂Γ/∂Wj-1,j就二者相乘就好! 這就是反向傳播的原理。 Reference : (深度學習之父Hinton的反向傳播教學) (4) Lecture 3.4 - The backpropagation algorithm - [ Deep Learning | Geoffrey Hinton | UofT ] - YouTube
