【QA】代價函數到底是什麼? 跟損失函數不一樣嗎?
代價函數(Cost Function)是定義在整個訓練集上的,是所有樣本誤差的平均,也就是損失函數的平均。 此篇主要介紹代價函數的作用及原理, 常見代價函數, 代價函數為甚麼需要非負及用Cross Entropy代替二次代價函數的原因。 為什麼需要代價函數?
回答列表
-
2021/11/10 下午 01:36Kevin Luo贊同數:0不贊同數:0留言數:0
為了獲得訓練邏輯回歸模型的參數,需要一個代價函數,透過訓練代價函數來得到參數,用於找到最佳解的目的函數。 代價函數的作用原理: 在回歸問題中,透過代價函數求最佳解,常用的是平方誤差代價函數。 假設函數的image如下圖所示: 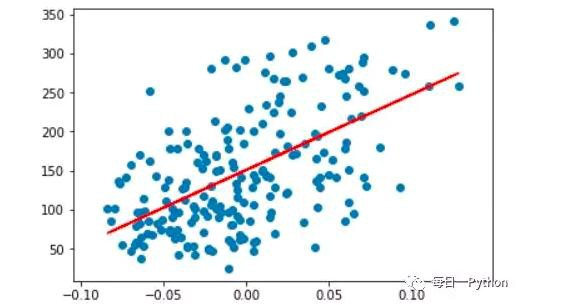 當參數發生變化時,假設函數狀態也會隨著變化。 想要擬合圖中的Scatter點,我們盡量要可能找到最佳參數來使這條直線更能代表所有資料。如何找到最佳解呢?這就需要用到代價函數來求解,以平方誤差代價函數為例,假設函數為h(x)=θx, 途中代表函數為y = Ax+B。 平方誤差代價函數的中心思想是將實際資料列出的值與擬合出的線對應到的值做相減(差),求出擬合出的直線與實際的差距。 在實際應用中,為了避免因為個別的極端資料產生的影響,要採用方插再取1/2的方式來減低個別資料的影響。 因此,會引出下面這個代價函數。 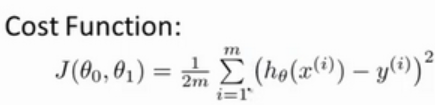 最佳解即為代價函數的最小值: 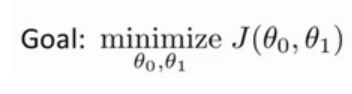 如果是1個參數,代價函數一般透過二維曲線便可直接觀察出。 但如果是2個參數,那麼透過3D的影像可看出代價函數的效果。 參數越多,越複雜。 當參數維2個時,代價函數為3D影像,如下圖。 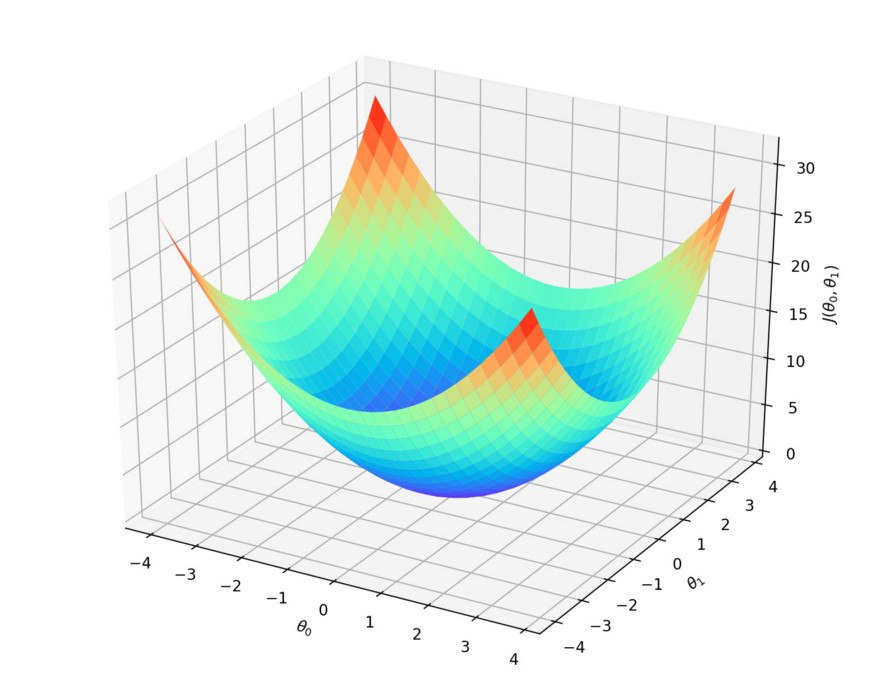 常見的代價函數: 二次代價函數(Quadratic Cost): 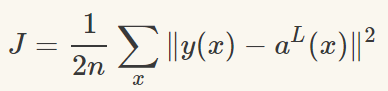 其中,J表示代價函數,x表示樣本,y表示實際值,a表示輸出值,n表示樣本的總數。使用一個樣本為例簡單說明,此時二次代價函數為: 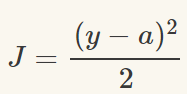 假如使用梯度下降法(Gradient descent)來調整權值參數的大小,權值w和偏置b的梯度推導如下: 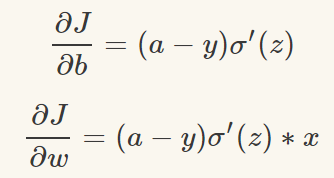 其中,z表示神經元的輸入,a=σ(z)其中z=wx+b,σ表示啟動函數(Activation Function)。權重w和偏值b的梯度跟啟動函數的梯度成正比,啟動函數的梯度越大,權值w和偏置b的大小調整得越快,訓練收斂得就越快。 注意: 神經網路常用的啟動函數為sigmoid函數,如下圖。 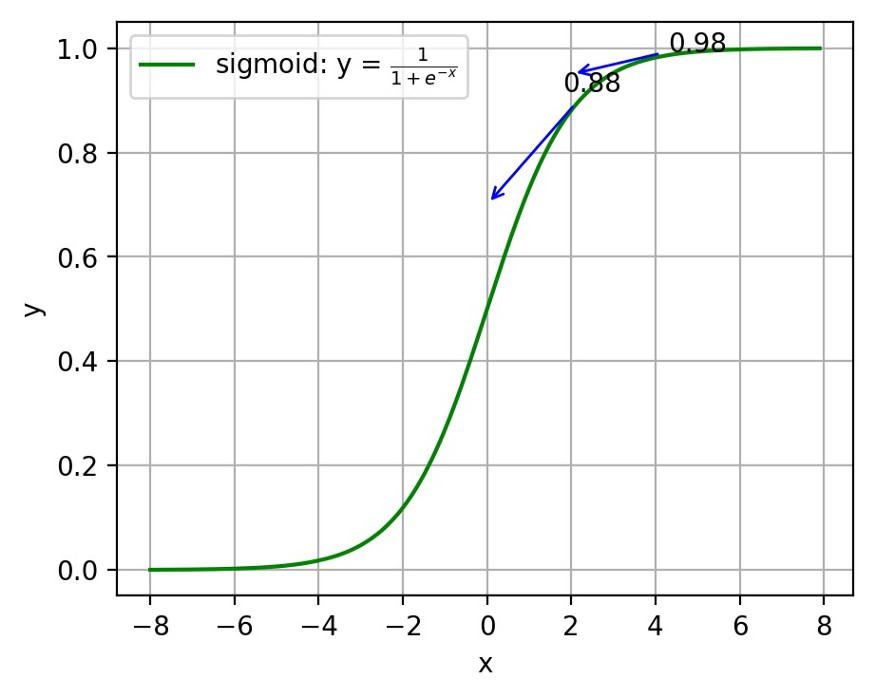 如上圖所示,我們對0.88和0.98兩個點進行比較: 假設目標是收斂到1.0。 0.88離目標1.0比較遠,梯度比較大,權重調整比較大。 0.98離目標1.0比較近,梯度比較小,權值調整比較小。 調整方案合理。 假如目標是收斂到0。 0.88離目標0比較近,梯度比較大,權值調整比較大。 0.98離目標0比較遠,梯度比較小,權值調整比較小。 調整方案不合理。 原因:在使用sigmoid函數的情況下, 初始的代價(誤差)越大,導致訓練越慢。 交叉熵代價函數(cross-entropy): 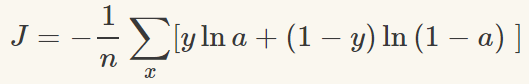 其中,J表示代價函數,x表示樣本,y表示實際值,a表示輸出值,a=σ(z)其中z=wx+b,n表示樣本的總數。 權重w和偏值b的梯度推導如下: 推導公式時需要用到Sigmod函數一基本性質: 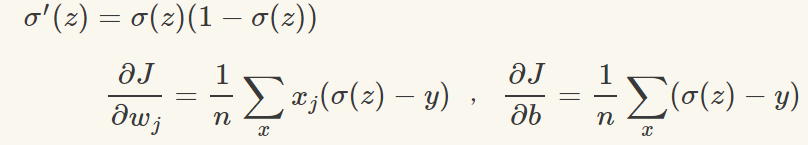 當誤差越大時,梯度就越大,權重w和偏值b調整就越快,訓練的速度也就越快。 二次代價函數適合輸出神經元是線性的情況,交叉熵代價函數適合輸出神經元是S型函數的情況。 對數似然代價函數(log-likelihood cost): 對數似然函數常用來作為softmax回歸的目標函數。 深度學習中普遍的做法是將softmax作為最後一層,此時常用的代價函數是對數似然代價函數。 對數似然代價函數與softmax的組合和交叉熵與sigmoid函數的組合非常相似。 對數似然代價函數在二分類時可以化簡為交叉熵代價函數的形式。 **為什麼目標函數是負的:** 目標函數存在一個下界,在優化過程當中,如果優化演算法能夠使目標函數不斷減小,根據單調有界準則(一種優化方法),這個優化演算法就能證明是收斂有效的。 只要設計的目標函數有下界,基本上都可以,代價函數非負更為方便。 為什麼用交叉熵代替二次代價函數: (1)為什麼不用二次方代價函數 假設權重w和偏值b的偏導數為∂J/∂w=(a−y)σ′(z)x和,∂J/∂b=(a−y)σ′(z), 偏導數受啟動函數的導數影響,sigmoid函數導數在輸出接近0和1時非常小,導數小,差值error也小,會導致一些實例在剛開始訓練時學習得非常慢。 (2)為什麼要用交叉熵 交叉熵函數權重w和偏值b的梯度推導為: 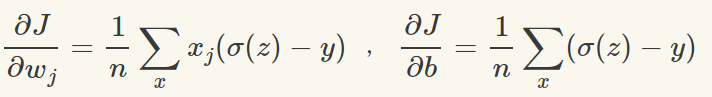 由以上公式可知,權重學習的速度受到σ(z)−y影響,更大的誤差,就有更快的學習速度,避免了二次代價函數方程中因σ′(z)導致的學習緩慢的情況。
