【QA】一維卷積(1D Convolution)的卷積方法?
上次在[【QA】一維卷積、二維卷積、三維卷積之間的差異?? 回答 1](https://www.cupoy.com/qa/club/ai_tw/0000016D6BA22D97000000016375706F795F72656C656173654B5741535354434C5542/0000017C095875A4000000286375706F795F72656C656173655155455354)中已經大致說明了一維卷積的概念,本次要進一步介紹一維卷積(1D Convolution)的卷積方法
回答列表
-
2021/09/23 下午 05:40Ray贊同數:0不贊同數:0留言數:0
上次在[【QA】一維卷積、二維卷積、三維卷積之間的差異?? 回答 1](https://www.cupoy.com/qa/club/ai_tw/0000016D6BA22D97000000016375706F795F72656C656173654B5741535354434C5542/0000017C095875A4000000286375706F795F72656C656173655155455354)中已經有提到過了一點一維卷積的概念了,這次我們進一步去了解一維卷積的卷積計算方法,我們已經了解了一維卷積的輸入、輸出、filters都是一個向量,而一維卷積的一維是指filter只能往一個方向移動,其輸入與輸出皆是二維。 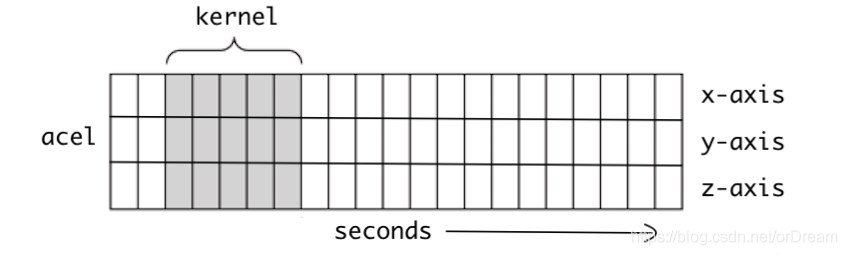[參考圖片來源](https://blog.csdn.net/orDream/article/details/106342711) 接著我們要來介紹一維卷積的卷積計算原理,我們以語音識別為例。語音中是按幀來進行處理的,每一幀都有相對應的特徵向量,常用的特徵向量有MFCC等,通常處理完一幀得到的是一個39維的MFCC特徵向量。假設一段語音有N幀,處理完這段語音後得到的是一個39行N列(行表示特徵維度,列表示幀數)的矩陣,我們將這個平面卷積作為一維卷積的輸入。沒錯,一維卷積的輸入並不一定要像我們之前舉例的一樣,只能有一行,但是filters的移動方向一定只能有一個 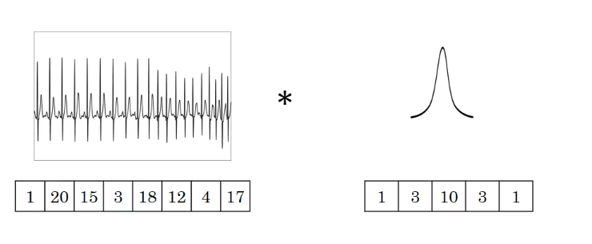[參考圖片來源](https://blog.csdn.net/qq_37555071/article/details/107541194) 因此假設filters是一個矩陣(J行K列)而輸入為39行N列,則J = 39,輸入與filters的行數一定相同,所以在描述filters時只需要知道kernel size(即多少列)和filters的數量就好了。 知道kernel size和kernel count後,再來看一維卷積的計算過程,看一個輸入矩陣經過一維卷積後得到的是什麼。設padding為same(卷積處理後的輸出與輸入的列數相同,而行數則是受filter的個數影響,若是二維卷積則大小相同),stride為1(kernel一次只移動一格)。假定輸入矩陣為3x5的矩陣,filters個數為2,kernel size為3,所以kernel是一個3x3的矩陣。輸入矩陣和兩個kernel矩陣的具體值如下圖,兩個kernel的bias分別是2和3。 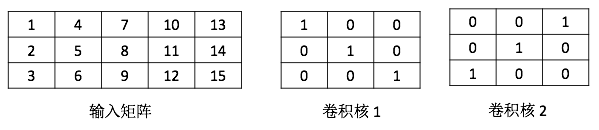[參考圖片來源](https://www.cnblogs.com/talkaudiodev/p/14287562.html) 先看第一個卷積核與輸入矩陣的計算。由於padding模式是same,輸入矩陣左右都要都要補充1列(用0填充)。補充後輸入矩陣變成了下圖。 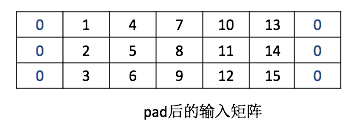[參考圖片來源](https://www.cnblogs.com/talkaudiodev/p/14287562.html) 做卷積時先從左邊的padding處開始,具體如下圖,相對應的位置相乘再相加後,再加上bias就可以了,計算出值為10(0 x 1 + 1 x 0 + 4 x 0 + 0 x 0 + 2 x 1 + 5 x 0 + 0 x 0 + 3 x 0 + 6 x 1 + 2 = 10)。 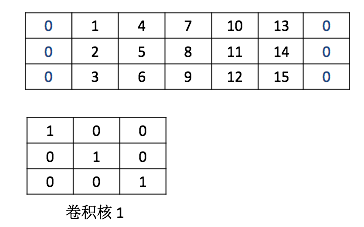[參考圖片來源](https://www.cnblogs.com/talkaudiodev/p/14287562.html) 接著依序向右移動,每次移動一格,經過4次的移動後就到了右邊的padding處,並使用同樣的方法進行計算。最終得到的是一個1行5列的矩陣,如下圖: [參考圖片來源](https://www.cnblogs.com/talkaudiodev/p/14287562.html) 第二個kernel的卷積計算與第一個kernel計算一樣,得到的也是一個1行5列的矩陣。如下圖: 最終一個3x5的輸入矩陣與filters個數為2、kernel size為3的矩陣進行卷積操作後得到的是一個2行5列的矩陣,如下圖。 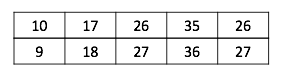[參考圖片來源](https://www.cnblogs.com/talkaudiodev/p/14287562.html) 可以看出卷積後輸入矩陣的列數不變,行數則與filters的個數相同(這是在padding模式為same、stride為1的case下,其他條件下雖然行數依舊是filters的個數,但列數會有所變化,比如stride > 1 或者用上maxpooling後列數會減少,但卷積計算過程是一樣的) ------------------------ 有興趣進一步了解的人可以參考以下連結: * [理解1D、2D、3D卷积神经网络的概念](https://blog.csdn.net/orDream/article/details/106342711) * [多維卷積與一維卷積的統一性(運算篇)](https://www.itread01.com/content/1546649488.html) * [一维卷积与多维卷积概念介绍(一)](https://www.jianshu.com/p/7eb0fa5517c0) * [一维卷积神经网络_卷积神经网络中的计算](https://blog.csdn.net/weixin_39906521/article/details/110814034) * [卷积神经网络中一维卷积的计算过程](https://www.cnblogs.com/talkaudiodev/p/14287562.html)
