【QA】如何透過梯度下降法(Gradient Descent )優化技術找出最優的模型?
在神經網絡中,所謂最優的模型,就是指說其Loss function 值最小的模型,而我們該做的就是讓模型自己透過優化(optimizer)的機制,找出這個Loss function 最小的模型。 而在機器學習或是神經網絡的世界中,最基本的優化方式就是梯度下降法(Gradient Decent ),而下面我想跟大家簡單討論一下,梯度下降法是如何運作,並找出最優的模型參數的。
回答列表
-
2021/08/16 下午 11:39Chili贊同數:0不贊同數:0留言數:0
梯度即為微積分的一階微分,而這簡單的概念,就讓模型參數能有所依據做更新,找到函數局部最小值。 * 微分: 這裡先來介紹一下一階微分,假設這裡有一個兩次方(二維的)方程式,我們可以透過對其做一階微分,近一步找到方程式上任一點的切線斜率,當切線斜率為0時,該點即為該方程式的最小值。 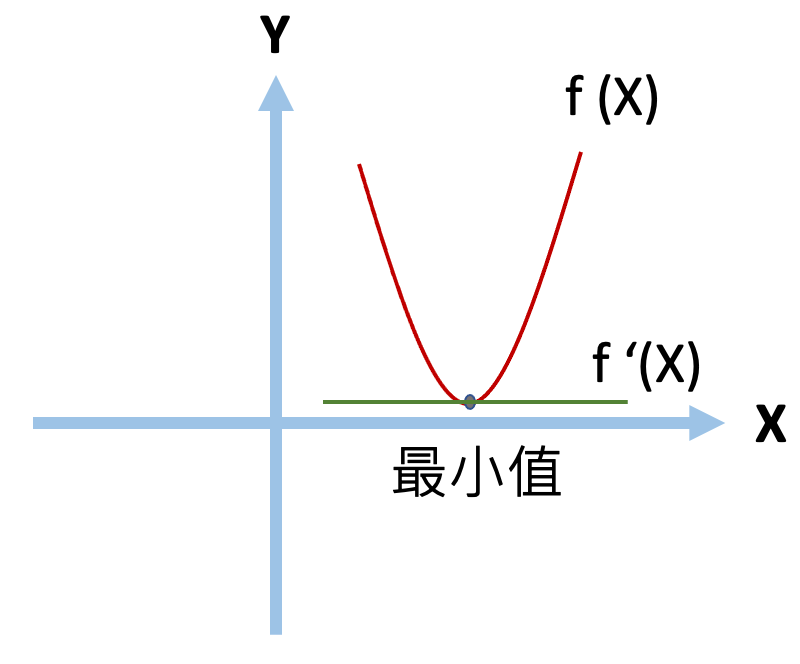 *f (x)為原本二次方函數 *f ‘(x)為一階微分的導函數。 --- * 而我們需要如何透過對X找到Y的最小值呢? 首先,我們先隨便找一個點,並找出該點斜率,並針對其一階微分後的結果做方向上面的調整。 公式如下: 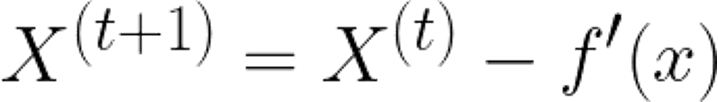 當我們找到一個點後,將他扣除掉自己一階導函數的值,即可以在方向上做更新。(下面用圖來說明) --- * 當一開始X斜率為正時(點會往左邊移動): 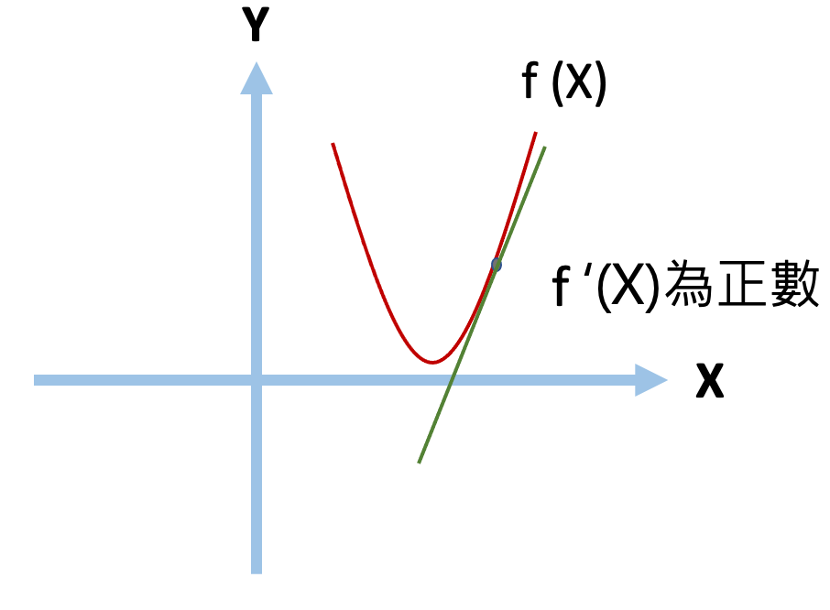 我們將其原本X值減上自己一階微分過後的值後,可以得到一個向左移動,接近最小值的點。 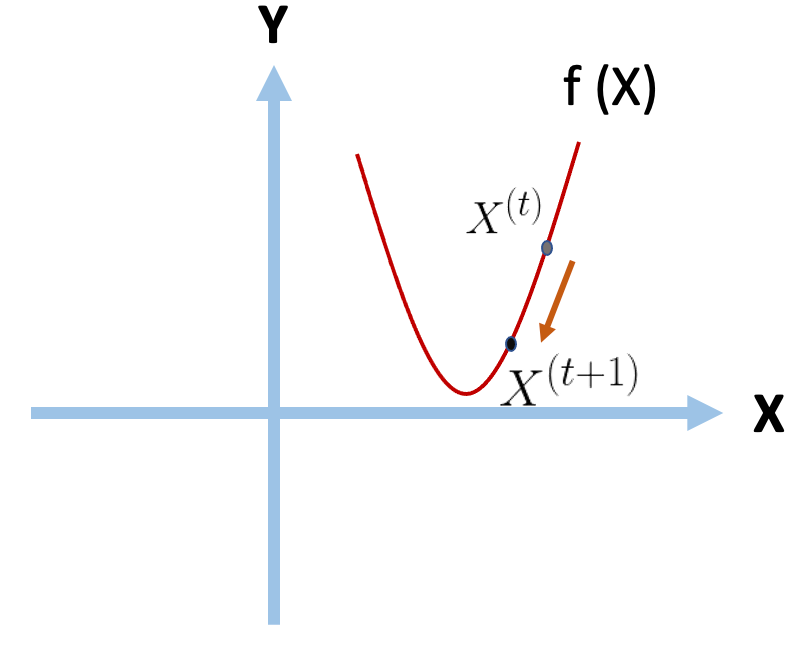 --- * 當一開始X斜率為負時(點會往右邊移動): 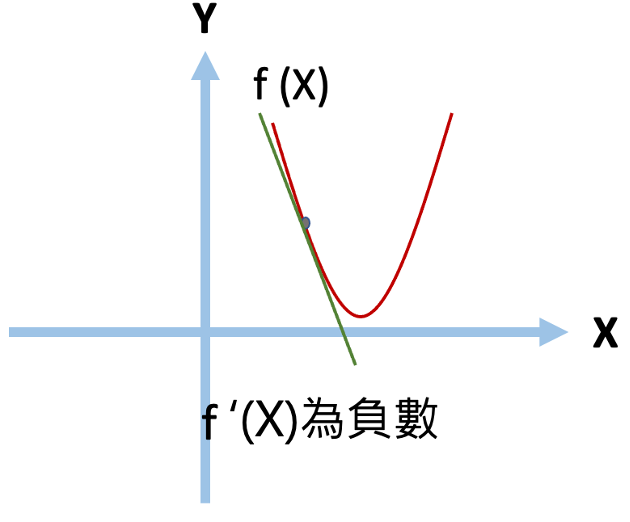 我們將其原本X值減上自己一階微分過後的值後,可以得到一個向右移動,接近最小值的點。 (fs>18:_(減掉負數相當於加上正數)_
