如何使用DBScan處理資料的離群值(Outlier) ?
先解釋一下離群值對機器學習的影響: 離群值的發生通常是因為資料輸入時發生誤植、筆誤,也有可能是某個群體內的少數特例。在這樣的情況下,離群值的存在會破壞整個樣本的一致性,就像是壞了一鍋粥的那粒老鼠屎一樣,它會影響機器學習的效果還有預測的準確性,導致分析後的結果難以解釋。 離群值不是只有負面的影響,它在某些特殊的應用場景扮演了非常重要的角色,例如疾病預測,如果一個人身上有些特殊的指標產生異常,或是一群人中有一小群人發生了異常生理現象(好比目前Covid19的疫情初期),這類的離群值就是一個非常重要的起點。 這類的情況也常用在網路詐騙、信用卡盜刷、網路攻擊等情況,整體來說,就是有一小群特別的資料,但會對整個群體產生重大影響的異常資料,所以離群值的偵測和處理,無論在統計或資料科學,都是一個重要的議題。 DBScan 是一種非監督的分群學習法,看起來似乎可以用在outlier的分群上,具體可以怎麼作呢? 以下跟大家討論一下
回答列表
-
2021/07/21 下午 08:12Felix Pei贊同數:1不贊同數:1留言數:0
DBScan是一種Cluster base的算法,它基於數據間的密度進行分群,可以處理多維度的資料進,其它Cluster Base的算法如k-means也可以分群。 DBScan有3個重要的points ・Core Point(核心點) ・Board Point (邊界點) ・Noise Point (離群點) 先用一張示意圖表示: 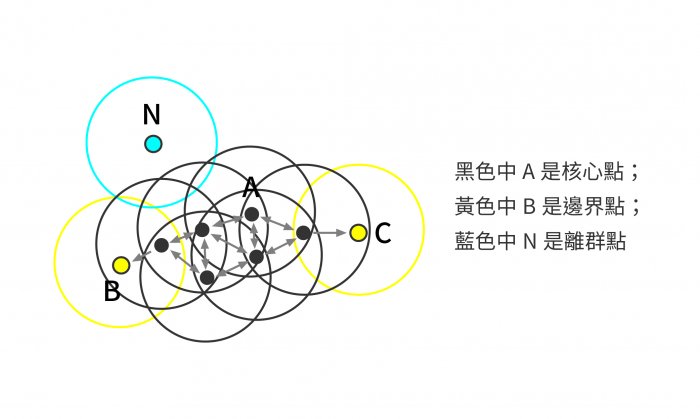 上面這些點是分佈在樣本空間的所有樣本,我們的目標是把這些在樣本空間中距離相近的歸類成一群。我們發現A點附近的點密度較大,黑色的圓圈根據一定的規則在這裡滾啊滾,最終收納了A附近的5個點,標記為黑色也就是定為同一個群(Cluster)。其它沒有被收納的根據一樣的規則成Cluster。 實務上我們在眾多樣本點中隨機選中一個點,圍繞這個被選中的樣本點畫一個圓,規定這個圓的半徑以及圓內最少包含的樣本點,如果在指定半徑內有足夠多的樣本點在內,那麼這個圓圈的圓心就轉移到這個內部樣本點,繼續去圈附近其它的樣本點,不斷滾來滾去的圈地,直到發現所圈住的樣本點數量少於預先指定的值,就停止了。那麼我們稱最開始那個點為核心點,如A,停下來的那個點為邊界點,如B、C,而最後沒圈到的那些點就是離群點,如N。 附上 python 程式碼給大家參考: ```python # %% # 使用DBScan進行分群 from sklearn.cluster import DBSCAN random_data = np.random.randn(50000, 2) * 20 + 20 # min_sample是要成為core point必需能圈進的樣本數 # eps是指core point為圓心的半徑長度 outlier_detection = DBSCAN(min_samples=2, eps=3) clusters = outlier_detection.fit_predict(random_data) list(clusters).count(-1) # %% # 使用Iris資料集進行DBScan分群 import matplotlib.pyplot as plt from sklearn import datasets from sklearn.cluster import DBSCAN iris = datasets.load_iris() X = iris.data X = X[:, 2:4] clustering = DBSCAN(eps=0.3, min_samples=10).fit(X) # 其中-1的資料就是離群值 clustering.labels_ #列出離群值的數組 outlier_idxes=np.where(clustering.labels_==-1) X[outlier_idxes] ``` 關於DBScan的優缺點整理如下: 優點: 1.可以對任意形狀的稠密數據集進行分群,相對的,K-Means之類的算法一般只適用於凸數據集。 2.可以在分群的同時發現異常點,對數據集中的異常點不敏感。 3.分群結果沒有偏倚,相對的,K-Means之類的算法,初始值對分群結果有很大影響。 缺點: 1.如果資料集的密度不均勻、分群間距差相差很大時,分群質量較差,這時不太適合用DBSCAN分群。 2.如果資料集較大時,Cluster收斂時間較長 3.調參相對於傳統的K-Means之類的分群算法稍復雜,主要需要對距離閾值eps,鄰域樣本數閾值Min-points聯合調參,不同的參數組合對最後的分群效果有較大影響。
